The challenge is about a method developed by the author to check if his passwords have been leaked, with constraints to avoid the storage of these passwords in plaintext.

This is an echo of the web site Have I Been Pwned, in which any user can check if credentials have been leaked for a given e-mail address.

Challenge Discovery

The source code of the server and the client are given to the challengers. They are written in Sage (a Python framework used for doing mathematical stuff in a more abstract way). Here is what it looks like:

Server

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81

#!/usr/bin/env sage
from common import *
from Crypto.Random import random
import json
import threading
import socket

with open("passwords", 'r') as f:
    passwords = f.read().strip().split('\n')

class Server:
    CHUNK = 64
    def __init__(self, host='0.0.0.0', port=31337):
        print(f"Binding to {host}:{port}")
        self.s = socket.socket()
        self.s.bind((host, port))

    def listen(self):
        self.s.listen(5)
        while True:
            c, addr = self.s.accept()
            threading.Thread(target=self.puzzle, args=(c,)).start()

    def puzzle(self, conn):
        c = conn
        def send(msg):
            c.sendall((msg + '\n').encode())
        def recv():
            message = b''
            while len(message) < 4098:
                part = c.recv(self.CHUNK)
                if b'\n' in part:
                    message += part.split(b'\n')[0]
                    break
                else:
                    message += part
            return message
        try:
            xs = []
            ys = []
            bs = []
            m = xy_to_curve(*json.loads(recv()))
            for i in range(len(passwords)):
                b = sample_R()
                p = b * base_p
                bs.append(b)
                key = F(md5(passwords[i].encode()))
                px, py = p.xy()
                xs.append((key, px))
                ys.append((key, py))
            x_poly = R.lagrange_polynomial(xs)
            y_poly = R.lagrange_polynomial(ys)
            send(str(x_poly))
            send(str(y_poly))
            ks = set(json.loads(recv()))
            if len(ks) > 20:
                send("Error: password limit exceeded.")
                return

            intersection = []
            for p, b in zip(passwords, bs):
                elem = sha(p.encode() + str((b * m)).encode()).hex()
                if elem in ks:
                    intersection.append(p)

            if len(intersection) == len(passwords):
                send("They've all been pwned?! Really?!?! Please hold my flag while I go change them.")
                with open("flag", "r") as f:
                    send(f.read())
            elif len(intersection) != 0:
                send("Some of my passwords have been leaked! I'll change them when I get around to it...")
            else:
                send("It's good to know that none of my passwords are in your pwned database :)")
            c.shutdown(1)
            c.close()
        except Exception as e:
            pass

if __name__ == "__main__":
    server = Server()
    server.listen()

Client

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

#!/usr/bin/env sage

from common import *
import json
import socket
import sys

IP = "hav3-i-b33n-pwn3d.damctf.xyz"
PORT = 30944
CHUNK = 64

def send(c, msg):
    c.sendall((msg + '\n').encode())

def recv(c):
    message = b''
    while len(message) < 4098:
        part = c.recv(CHUNK)
        if b'\n' in part:
            message += part.split(b'\n')[0]
            break
        else:
            message += part
    return message.decode()

def main():
    passwords = sys.argv[1:]
    a = sample_R()
    m = a*base_p
    s = socket.socket()
    s.connect((IP, PORT))
    send(s, str(list(m.xy())))
    x_poly = R(recv(s))
    y_poly = R(recv(s))
    if x_poly.degree() < 1 or y_poly.degree() < 1:
        exit(1)
    ks = []
    for pas in passwords:
        key = F(md5(pas.encode()))
        px = x_poly(key)
        py = y_poly(key)
        point = xy_to_curve(px, py)
        k = sha((pas + str(a * point)).encode())
        ks.append(k.hex())
    crypt_random.shuffle(ks)
    send(s, json.dumps(ks))
    print(recv(s))

if __name__ == "__main__":
    main()

Utilities

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

#!/usr/bin/env sage
from sage.all import *
from sage.schemes.elliptic_curves.ell_point import EllipticCurvePoint_number_field
from Crypto.Hash import MD5, SHA256
from Crypto.Random import random as crypt_random

curve25519_p = 2**255 - 19
F = GF(curve25519_p)
R = F['x']
x = R.gen()
curve25519 = EllipticCurve(F, [0, 486662, 0, 1, 0])
#assert(curve25519.count_points() == 57896044618658097711785492504343953926856930875039260848015607506283634007912)

# cofactor == bad?
def sample_R():
    return (crypt_random.randrange(2**255) >> 3) <<3

def md5(msg: bytes) -> int:
    h = MD5.new()
    h.update(msg)
    return int.from_bytes(h.digest(), 'little')

def sha(msg: bytes) -> bytes:
    h = SHA256.new()
    h.update(msg)
    return h.digest()

def xy_to_curve(x, y):
    return EllipticCurvePoint_number_field(curve25519, (x, y, 1), check=False)

base_p = xy_to_curve(9, 43114425171068552920764898935933967039370386198203806730763910166200978582548)

Algorithm analysis

Diffie Hellman over Elliptic Curve

This part is not necessary for understanding the overall resolution. Therefore, if you do not understand everything, no worry, you can skip it (or you can PM me if you wish to have more details).

All the operations are done on an elliptic curve defined over a finite field. I spent quite a lot of time to see if there was any flaw (especially why the author did not use a classic curve). Apparently it was a rabbit hole, as the same curve was used in another challenge (so it probably has no trivial vulnerability to exploit). However, it is interesting to see that the order of the curve (the number of points defined on this curve over the finite field) is a product of 8 and a larger factor. As it could induce some major flaws if the numbers are badly chosen, it is necessary to ensure that they are a multiple of 8 (by using 3-bit shifting). This condition ensures the numbers chosen are not in the smallest subfield.

1
2
3
4
5
6
7
8

# function used to generate safe numbers for the finite field of size 2**255 - 19
# The operation (n >> 3) << 3 is used to erase the 3 least significant bits, meaning the result is a multiple of 2**3 = 8
def sample_R():
    return (crypt_random.randrange(2**255) >> 3) <<3

factor(curve25519.count_points())
# 2**3 * 7237005577332262213973186563042994240857116359379907606001950938285454250989
# Order of the curve. It is a product of 8 and a larger prime. By selecting numbers multiple of 8, there is no risk of falling under the subfield of size 8.

The application uses the elliptic curve to transmit secrets in a public environment, between two parties. In order to do that, it uses the Diffie Hellman key exchange over Elliptic Curves.

The Diffie Hellman algorithm allows parties to agree on a common secret thanks to the Discrete Logarithm Problem. In Elliptic Curves defined over finite fields, this problem works as follows: Let’s imagine the secret is the number b. Let’s use an arbitrary point P on the curve. If one transmits the new point Q = b*P, an attacker can intercept Q. As P is also public, In order to retrieve b, the attacker must find it by calculating it such that b*P = Q This problem is, still nowadays, hard to solve, as there is no easy way of “dividing” Q by P (which would let the attacker find b).

As a result, the Diffie Hellman protocol over Elliptic curves works as follows: the two parties A and B agree on the Elliptic Curve to chose (and the Finite Field used for defining points over it). They also agree on a base point P on this curve. Then, they chose random numbers in the finite field (a for A and b for B). They transmit to each other Pa = a*Pand Pb = b*P . Finally, they calculate S = a*b*P = a*Pb = b*Pa = b*a*P

An attacker can get Pa and Pb but, in order to get S, they must retrieve either a or b, which means they have to solve the Discrete Logarithm Problem.

The hard and technical part is finished, let’s dive into the challenge.

Communication analysis

By analyzing these files, it is possible to understand how the check of the passwords works:

The public data of the algorithm is:

• The finite field F of size p = 57896044618658097711785492504343953926634992332820282019728792003956564819949

• The curve curve25519 defined by the equation E: y**2 = x**3 + 486662*x**2 + x over F

• The point base_p on curve curve25519, of coordinates x = 9, y = 43114425171068552920764898935933967039370386198203806730763910166200978582548

The protocol is:

1. First, the client choses a secret a and transmits the point m = a*base_p
2. The server receives the point m
3. For each password:
   1. The server choses a secret b_i and calculates p_i = b_i * base_p
   2. The server calculates key_i = bytes.to_int(md5(password), "little endian")
   3. The server calculates m_i = b_i * m
   4. The server calculates el_i = sha256(password | str(m_i)) with | the string concatenation operator and str(m_i) a string representation of the point p_i
4. Once in possession of the list of keys and secrets, the server calculates two Lagrange polynomials (over the finite field F):
   1. x_poly, such that for each i, x_poly(key_i) = p_i.x
   2. y_poly, such that for each i, y_poly(key_i) = p_i.y
5. The server sends the two polynomials to the client
6. for each password given by the client:
   1. The client calculates key_i = bytes.to_int(md5(password), "little endian")
   2. The client calculates the points p_i by using the fact that x_poly(key_i) = p_i.x and y_poly(key_i) = p_i.y
   3. The client calculates Q_i = a * p_i
   4. The client generates the hash k_i = sha256(password | str(Q_i)) with | the string concatenation operator and str(Q_i) a string representation of the point Q_i
7. The client sends all the k_i hashes
8. The server receivers the k_i hashes.
9. The server checks the intersection of the k_i hashes and the el_i hashes.
   1. If both sets are equal, it sends back the flag.
   2. If the intersection is not empty, the server sends back a message of “passwords being compromised”
   3. If the intersection is empty, the server sends back a safe message.

This algorithm works thanks to the Diffie Hellman key exchange algorithm. Indeed, for each password, Q_i = a * p_i = a * b_i * p = b_i * a * p = b_i * m = m_i.

The Lagrange polynomials are here to send the public points corresponding to each password. Indeed, a Lagrange polynomial P is a polynomial defined by couples (x_i, y_i), such that for each i, P(x_i) = y_i . In this case, the Lagrange polynomials x_poly and y_poly are defined by the following couples: for each key_i derived from the passwords, for each p_i associated to the password, x_poly(key_i) = p_i.x andy_poly(key_i) = p_i.y. This allows to transmits the coordinates x and y of each point separately.

Therefore, the client will be able to calculate the right SHA256 sums only if they find the right coordinates of each point, and this is doable only if they find the right keys derived from each password.

By the way, the Lagrange polynomial degree is defined by the number of couples used for its generation. Here, the degree is 15, meaning 16 passwords are tested.

Spot the flaw

In order to find the vulnerability, the first step is to eliminate the possible rabbit holes.

examinate the SHA256 sum

The final hashes are defined by sha256(password | str(Q_i).

This means that, in order to find it, the user must already have the right password. Plus, the string representation of each point is hard to calculate without finding the associated points.

As a result, there is no vulnerability here.

Retrieving the public points

In order to retrieve the public points, the user must get the right md5 sums corresponding to passwords. As a result, retrieving the points means the user has already found the MD5 sums.

Once the rabbits holes identified it is possible to focus on the main point of the program: the Lagrange polynomials.

Exploiting the Lagrange Polynomials

It is interesting to see that every operation is done over the finite field F. This means that operations on the polynomials and on the elliptic curve can be combinated.

This leads to an hypothesis: is it possible to abuse the Lagrange polynomials and the curve equation to retrieve the points ?

Indeed, as defined, the Lagrange polynomials give valid points on the curve for the different MD5 hashed passwords. This means that, for any z in F, by settingx = x_poly(k) and y = y_poly(k), these satisfy the equation y**2 = x**3 + 486662*x**2 + x especially in the case of k = md5(password).

Therefore, by defining the polynomial k_poly(k) = x_poly(k)**3 + 486662 * x_poly(k)**2 + x_poly(k) - y_poly(k)**2, it is possible to retrieve the MD5 hashes by looking at the small roots of k_poly.

This can be done by slightly modifying the client script:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

#!/usr/bin/env sage
from common import *
import json
from pwn import remote
import sys
IP = "hav3-i-b33n-pwn3d.damctf.xyz"
PORT = 30944
IP = "localhost"
PORT = 31337

def main():
    a = sample_R()
    m = a*base_p
    while True:
        s = remote(IP, PORT)
        s.sendline(str(list(m.xy())))
        # the two Lagrange polynomials are retrieved here
        x_poly = R(s.recvline(s)[:-1].decode())
        y_poly = R(s.recvline(s)[:-1].decode())
        # Create k_poly, using the curve equation to have MD5 sums in the roots of the polynomial
        k_poly = x_poly**3 + 486662 * x_poly**2 + x_poly - y_poly**2
        roots = k_poly.roots()
        print(f"{roots = }")
        if len(roots) > 16:
            exit(0)

if __name__ == "__main__":
    main()

The result of the program is:

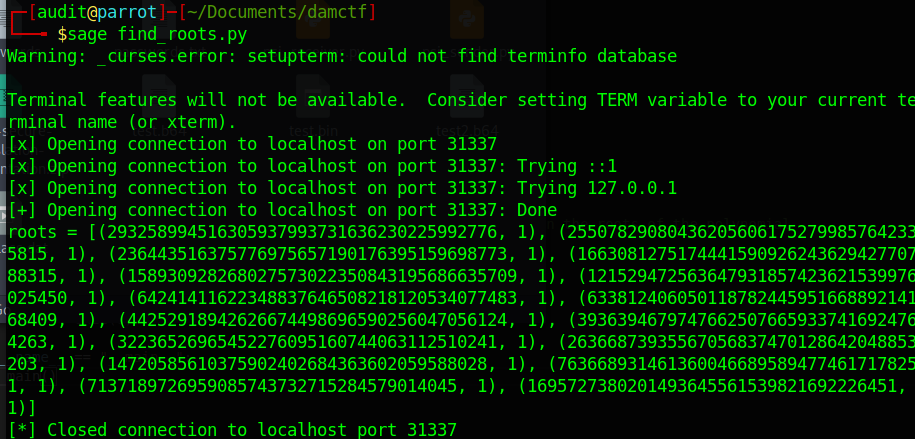
Breaking the MD5 hashes

The program above gives the following small roots:

1

>>> roots = [(293258994516305937993731636230225992776, 1), (255078290804362056061752799857642335815, 1), (236443516375776975657190176395159698773, 1), (166308127517444159092624362942770788315, 1), (158930928268027573022350843195686635709, 1), (121529472563647931857423621539976025450, 1), (64241411622348837646508218120534077483, 1), (63381240605011878244595166889214168409, 1), (44252918942626674498696590256047056124, 1), (39363946797476625076659337416924764263, 1), (32236526965452276095160744063112510241, 1), (26366873935567056837470128642048853203, 1), (14720585610375902402684363602059588028, 1), (7636689314613600466895894774617178251, 1), (7137189726959085743732715284579014045, 1), (1695727380201493645561539821692226451, 1)]

Converted into bytes (little endian), it gives the following hashes:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

>>> print("\n".join([int.to_bytes(x[0], 16, "little").hex() for x in roots]))
481cf17a2f3a0cfafcedaa0dbea09fdc
476e90c539400f0e2988b32db64ae6bf
557d2cd9d61ebd645f0713ca655de1b1
db3715c800e019e84c7fea4dc0c71d7d
bdc87b9c894da5168059e00ebffb9077
6a951dee3380abc4b7aa2ccd9bb96d5b
2bb051b27a55de60f1b3550022725430
594dbf2c9321c4424b8e38676dc8ae2f
fce4765160cd540d146acd215bcd4a21
67983c8501b3aae0ba8179426b389d1d
21fb2e1c8d19182c1602897d7d874018
d3040380b07cc31250d18aa64013d613
bcf1bf1fe1b2de521306fad6e714130b
8b8037d5ca8f3c84363d7354dac5be05
9dd530606c2930dd60310d2e9f925e05
938b47219ea281812a031694d0954601

All these hashes can be cracked using Crackstation:

Getting the flag

The last step is just to send the passwords to the server, which then gives back the flag:

And here is the flag:

dam{I_DoN'T_KnOw_1f-i-wAs-pwN3D_8U7-1_$ur3-@M-nOW}